プロジェクト
tinker.
experiments_

From Scratch: MNIST Digit Recognizer
First time building a neural network
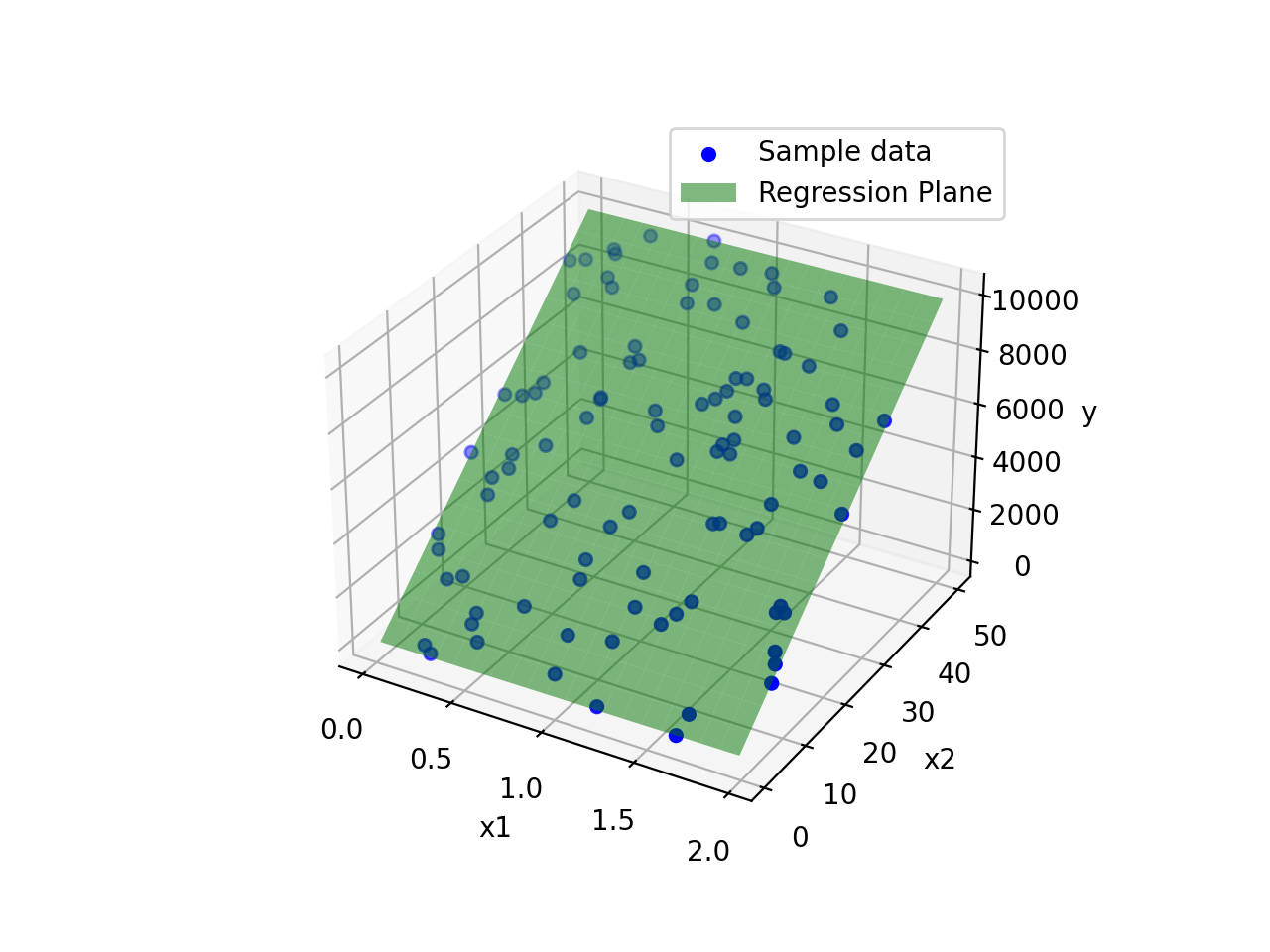
From Scratch: Linear Regression
Learning regression and gradient descent

Liquid-Vapor Transitions
Implementing Kawasaki and Glauber models
engineering_
Memorable projects brought to life.
software_
Crafting digital experiences.
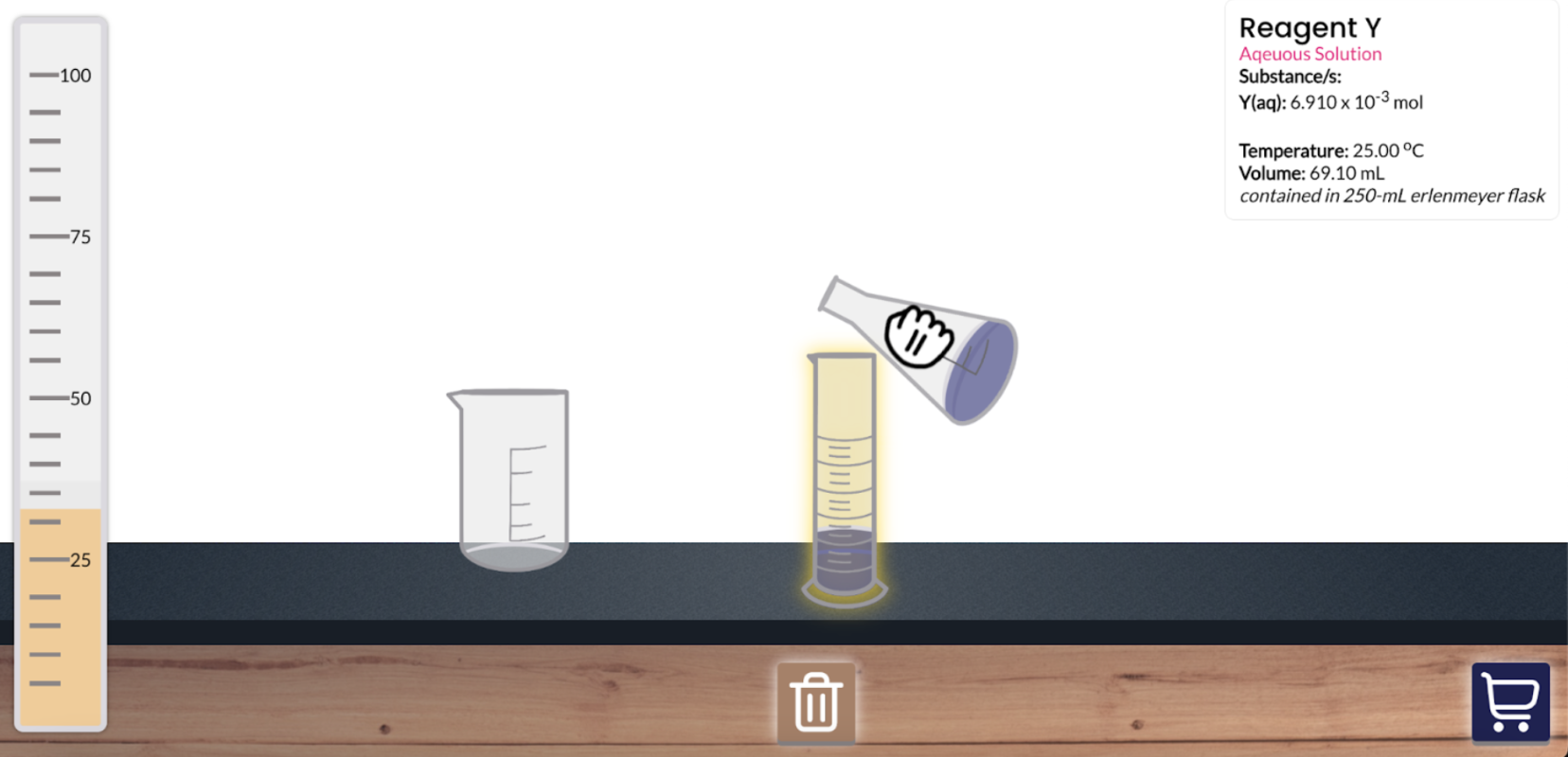
Chemaya
Hands-on virtual chemistry

Operation: Haunted
A retro metroidvania game built from scratch in Java.

Space Jam
Where my coding journey began
papers_
A collection of my highschool research and works (primarily in mathematical modeling).
1 / On Classification of Noiseless and Noisy Pattern Orientations
(2024)
🏆 Winner of the Distinction and Novelty Award at SIMC 2.0 2024. This paper presents our solution to a challenge problem in single-particle imaging. We developed deterministic and heuristic techniques to cluster image orientations in both noiseless and noisy 2D datasets. Our key methods included perceptual image hashing for the noiseless data and a modified K-means algorithm for the noisy data.
2 / Common Practices of Pandemic Speakers and the Influence of the Virtual Modality
(2023)
📄 First-author paper published in the proceedings of the International Young Researchers Conference 2023. This communication studies paper investigates a novel demographic: public speakers who began their careers during the virtual-first environment of the COVID-19 pandemic. We analyzed how the online modality shaped their public speaking practices and techniques.
3 / Pandemics over Networks
(2022)
🏆 High Distinction (Top 3, Junior Track) at SIMC 2.0 2022. This paper models the spread of a hypothetical “duovid” virus across a community represented as a network, employing a multi-level approach based on network complexity. We began by deducing infection properties analytically for simple, lattice-like networks. As complexity increased, we utilized graph traversal algorithms to simulate the spread, culminating in the use of regression models with graph feature engineering to generate results for the most complex community structures.
4 / On Airplane Boarding and Disembarking
(2022)
🏅 Rank 9 Award at the International Mathematical Modeling Challenge (IMMC) 2022. In this paper, we developed a two-part model to analyze and optimize airplane passenger flow. For boarding, we created a computational Monte Carlo simulation to estimate times for various methods, accounting for randomized passenger parameters. For disembarking, we derived a closed-form formula to calculate the optimal deplaning time for any given aircraft configuration.
5 / On the Situation of Lake Mead
(2021)
🏅 Finalist Award at the High School Mathematical Contest in Modeling (HiMCM) 2021. This paper presents our comprehensive, three-part analysis of the Lake Mead water crisis. We first applied statistical methods to identify trends in the lake’s declining water levels, then developed a calculus-based model to estimate the remaining water volume. These findings culminated in a detailed proposal for a new wastewater recycling plant to address the issue.

